Unveiling The Mystery Of "x*x*x Is Equal To 2": A Comprehensive Guide
Introduction
In the world of mathematics, equations often serve as gateways to understanding deeper truths about numbers and their relationships. Among these equations, "x*x*x is equal to 2" presents a fascinating challenge that invites us to explore the realms of algebra, exponents, and even the concept of irrational numbers. This article aims to unravel the mystery behind this cubic equation, offering insights into its meaning, solutions, and applications. Whether you're a student, a math enthusiast, or simply curious about the beauty of mathematics, this guide will provide a clear and engaging explanation.
Understanding the Basics
What Does x*x*x Mean?
The expression "x*x*x" is a mathematical shorthand for multiplying the variable "x" by itself three times. In mathematical notation, this is written as \(x^3\), which means "x raised to the power of 3." This process is also referred to as "cubing" a number. For example, if \(x = 2\), then \(x^3 = 2 \times 2 \times 2 = 8\).
Now, let's consider the equation \(x^3 = 2\). This equation essentially asks us to find a number "x" such that when multiplied by itself three times, the result is 2. In simpler terms, we are solving for \(x\) in the equation:
- Aagmaalgives
- Securely Connect Remote Iot Vpc Raspberry Pi Free
- Pining For Kim By Trailblazer
- Remoteiot Vpc Ssh Raspberry Pi Download
- Sophie Rain Spiderman Video
Why Is This Equation Important?
The equation "x*x*x is equal to 2" may seem simple at first glance, but it holds profound implications in mathematics. It introduces us to the concept of cube roots and irrational numbers, which are fundamental to advanced mathematical studies. Moreover, solving this equation requires a systematic approach that involves isolating \(x\) and understanding the properties of exponents.
Steps to Solve the Equation
Step 1: Understanding the Equation
Let’s break down the equation \(x^3 = 2\). Here, \(x^3\) represents the cube of \(x\), and the equation states that this cube equals 2. To solve for \(x\), we need to find the cube root of 2. Mathematically, this can be expressed as:
\[ x = \sqrt[3]{2} \]This means that \(x\) is the number which, when cubed, gives 2. The cube root of 2 is an irrational number, meaning it cannot be expressed as a simple fraction and has a non-repeating, non-terminating decimal expansion.
- Tory Kittles Partner
- Joel Landau Net Worth
- Sophie Rain Spiderman Video Tutorial
- T Girl Sophie Real Name
- Daisy Melanin Viral Video Original Youtube
Step 2: Verifying the Solution
To verify that \(x = \sqrt[3]{2}\) is indeed the solution, we can substitute it back into the original equation:
\[ (\sqrt[3]{2})^3 = 2 \]Simplifying this, we get:
\[ x^3 = 2 \]This confirms that our solution is correct.
Exploring the Nature of the Solution
Rational vs. Irrational Numbers
One of the intriguing aspects of this equation is that its solution, \(\sqrt[3]{2}\), is an irrational number. Irrational numbers are numbers that cannot be expressed as a ratio of two integers. They have infinite, non-repeating decimal expansions. For example, the cube root of 2 is approximately 1.25992, but this is only an approximation. The true value extends infinitely without repeating.
Real and Imaginary Numbers
The equation \(x^3 = 2\) belongs to the realm of real numbers, but it also hints at the broader world of complex numbers. In some cases, cubic equations can have solutions that involve imaginary numbers (numbers involving the square root of -1). However, in this specific case, the solution \(\sqrt[3]{2}\) is purely real.
Applications in Real Life
While the equation \(x^3 = 2\) may seem abstract, it has practical applications in various fields:
- Engineering: Understanding cubic equations is crucial in designing systems that involve volume calculations, such as in fluid dynamics or structural engineering.
- Physics: Cubic relationships often appear in physical laws, such as those governing the behavior of gases or the motion of objects.
- Computer Science: Algorithms and data structures frequently involve solving equations similar to \(x^3 = 2\), especially in optimization problems.
Tools to Solve Cubic Equations
For those who wish to explore further, there are several tools available to solve cubic equations:
- Online Calculators: Websites and apps offer step-by-step solutions for cubic equations, making it easier to verify results.
- Mathematical Software: Programs like WolframAlpha or MATLAB can handle complex equations and provide detailed explanations.
- Manual Methods: Traditional algebraic techniques, such as factoring or using the cubic formula, can also be employed.
Conclusion
In this article, we have explored the equation \(x^3 = 2\) and its solutions. Through our discussion of exponents, cube roots, and irrational numbers, we gained a deeper understanding of the mathematical principles at play. This equation serves as a gateway to more advanced topics in mathematics, including complex numbers and algebraic structures.
To summarize:
- The equation \(x^3 = 2\) asks us to find a number \(x\) such that \(x \times x \times x = 2\).
- The solution to this equation is \(x = \sqrt[3]{2}\), an irrational number.
- This equation has applications in engineering, physics, and computer science.
- Various tools and methods are available to solve similar equations, both online and offline.
By unraveling the mystery of "x*x*x is equal to 2," we not only enhance our mathematical knowledge but also appreciate the beauty and complexity of numbers. Whether you're solving for \(x\) or exploring the broader implications of cubic equations, mathematics continues to offer endless opportunities for discovery and learning.
- Aagmaaltech
- Who Is Tory Kittles Wife
- Pinning For Kim
- Valvoline Coupon 25 Off
- Is Tory Kittles Married
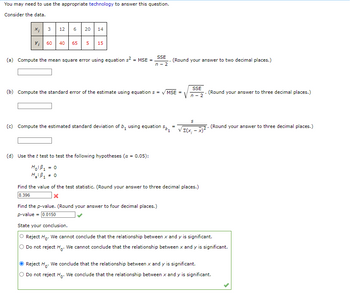
Answered: You may need to use the appropriate… | bartleby
XXXXXX-35 | Interminable Rooms Fan Ideas Wiki | Fandom
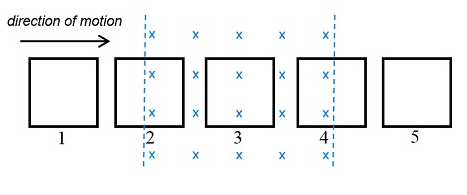
Solved x x xxxx x 1ххах. direction of motion direction | Chegg.com
