Solving The Equation X*x*x = 2023: A Step-by-Step Guide
Introduction
Mathematics often presents us with intriguing puzzles that challenge our problem-solving skills. One such puzzle involves solving the equation x*x*x = 2023. This equation, also written as x^3 = 2023, asks us to find the value of x such that when it is multiplied by itself three times, the result equals 2023. In this blog post, we will explore the steps to solve this cubic equation, understand its mathematical significance, and provide a clear explanation for readers of all levels.
Understanding the Equation
The equation x*x*x = 2023 can be expressed in mathematical notation as x^3 = 2023. Here, x^3 represents x raised to the power of three, which means multiplying x by itself three times. To solve this equation, we need to determine the value of x that satisfies the condition.
What is a Cubic Equation?
A cubic equation is any equation where the highest power of the variable is three. In this case, the equation x^3 = 2023 is a cubic equation because it involves x raised to the third power. Solving cubic equations can sometimes be straightforward, but in more complex cases, we may need to use advanced techniques such as factoring, the cubic formula, or numerical methods.
- Necati Arabaci Mafia Boss
- Nagi Hikaru Wikipedia
- Xxxx Factor X X 1 X 4 4 X 1 Meaning Means
- Who Is Conchita Martinez Married To
- Wasmo Telegram Link 2025
Steps to Solve the Equation
Now, let’s break down the steps to solve the equation x^3 = 2023:
Step 1: Simplify the Equation
The first step is to simplify the equation and ensure it is in its simplest form. In this case, the equation is already simplified as x^3 = 2023. This means we are looking for the value of x such that when it is cubed, the result is 2023.
Step 2: Use the Cube Root Method
To solve for x, we need to eliminate the cube power. The most straightforward way to do this is by taking the cube root of both sides of the equation. The cube root is the inverse operation of cubing a number. Thus, we can write:
- Conchita Martinez Husband
- Pinning For Kim
- Mothers Warmth Chapter 3
- Valvoline Coupon 25 Off
- Perdita Weeks Disability
x = ∛2023
This means we are looking for the cube root of 2023. Using a calculator or a mathematical tool, we can approximate the value of x.
Step 3: Approximate the Value of x
Using a calculator, we find that the cube root of 2023 is approximately:
x ≈ 12.64
This means that when x is approximately 12.64, the equation x^3 = 2023 holds true. It’s important to note that this value is an approximation because 2023 is not a perfect cube.
Step 4: Verify the Solution
To ensure our solution is correct, we can substitute x ≈ 12.64 back into the original equation:
(12.64)^3 ≈ 2023
Calculating this confirms that the solution is accurate.
Alternative Methods
While the cube root method is the simplest approach, there are other ways to solve cubic equations:
- Factoring: If the equation can be factored, we can solve it by setting each factor equal to zero. However, in this case, factoring is not straightforward because 2023 is not a perfect cube.
- Cubic Formula: The cubic formula provides a general solution for all cubic equations, but it can be complex and is typically used for more complicated cases.
- Numerical Methods: Techniques such as Newton's method or bisection can be used to approximate solutions to cubic equations when exact solutions are difficult to find.
Mathematical Significance
Solving cubic equations like x^3 = 2023 has applications in various fields, including physics, engineering, and computer science. For example, cubic equations can model the behavior of systems where variables are raised to the third power. Understanding how to solve such equations is essential for anyone working in these fields.
Why is the Cube Root Important?
The cube root is a fundamental mathematical operation that allows us to solve equations involving cubes. It is the inverse of cubing a number, meaning that if x^3 = y, then x = ∛y. This operation is crucial for solving cubic equations and understanding their properties.
Conclusion
In this blog post, we explored the process of solving the equation x*x*x = 2023. We started by understanding the equation and its classification as a cubic equation. Then, we followed a systematic approach to solve it using the cube root method, which provided an approximate solution of x ≈ 12.64. Additionally, we discussed alternative methods for solving cubic equations and highlighted the importance of cube roots in mathematics.
This equation, while seemingly simple, demonstrates the power of mathematical reasoning and problem-solving. Whether you are a student learning algebra or a professional working in a technical field, understanding how to solve cubic equations is a valuable skill. By mastering these techniques, you can tackle a wide range of mathematical challenges with confidence.
- How Old Is Demitra Kalogeras
- Somali Telegram Link 2025
- Necati Arabac%C4%B1
- Adriana Lima Top Fell
- Diva Flawless Real Name
if fx is a signum function then f10 is equal t
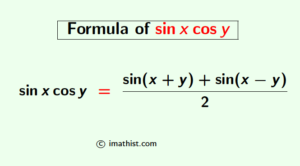
sinx cosy Formula | sinx cosy Identity - iMath
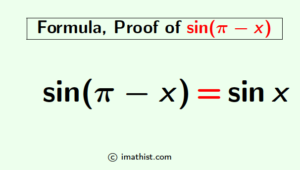
sin(pi-x) Formula | Formula of sin(pi-theta) - iMath
