Understanding The Equation "x*x*x Is Equal To 2": A Comprehensive Guide
Introduction
Mathematics is a field filled with intriguing challenges, and one such challenge is solving the equation "x*x*x is equal to 2." This seemingly simple equation hides a wealth of complexity and requires a deeper understanding of algebraic principles. In this article, we will delve into the meaning, solution, and applications of this equation, providing clarity for both beginners and advanced learners alike.
What Does "x*x*x is Equal to 2" Mean?
At its core, the equation "x*x*x is equal to 2" can be rewritten in mathematical notation as \( x^3 = 2 \). This means we are looking for a number \( x \) that, when multiplied by itself three times, equals 2. While this might seem straightforward, solving for \( x \) involves understanding the concept of cube roots and irrational numbers.
Breaking Down the Equation
- Step 1: Recognize the Form - The equation \( x^3 = 2 \) represents a cubic equation, where the variable \( x \) is raised to the power of 3.
- Step 2: Isolate \( x \) - To solve for \( x \), we need to isolate it on one side of the equation. This can be achieved by taking the cube root of both sides.
- Step 3: Solve for \( x \) - The solution to \( x^3 = 2 \) is \( x = \sqrt[3]{2} \), also known as the cube root of 2.
It's important to note that \( \sqrt[3]{2} \) is an irrational number, meaning it cannot be expressed as a simple fraction. Instead, it is represented as an infinite, non-repeating decimal. This adds to the complexity and intrigue of solving this equation.
- Maplestar
- Junko Furuta
- Buscar Kid
- Mydesinetcom
- %D0%BD%D0%B5%D0%BA%D0%B0%D1%82%D0%B8 %D0%B0%D1%80%D0%B0%D0%B1%D0%B0%D1%87%D0%B8
How to Solve \( x^3 = 2 \)
Solving the equation \( x^3 = 2 \) involves a systematic approach. Below, we outline the steps to arrive at the solution:
- Start with the Equation - Begin with \( x^3 = 2 \).
- Take the Cube Root - To isolate \( x \), apply the cube root operation to both sides of the equation: \( x = \sqrt[3]{2} \).
- Understand the Result - The result, \( \sqrt[3]{2} \), is an irrational number approximately equal to 1.25992.
This process highlights the importance of understanding cube roots and their role in solving cubic equations. While the solution may not be a whole number, it is a unique and intriguing mathematical constant.
Real-Life Applications
The equation \( x^3 = 2 \) might seem abstract, but it has practical applications in various fields:
- Securely Connect Remote Iot Vpc Raspberry Pi Aws Download Free
- Aagmaaltech
- Aldis Hodge Wife
- Joel Landau Net Worth
- How Old Is Demitra Kalogeras
- Engineering - Engineers often use cubic equations to model physical phenomena, such as stress distribution in materials.
- Physics - In physics, cubic equations can describe relationships between variables in systems like fluid dynamics or thermodynamics.
- Economics - Economists use cubic equations to analyze trends and predict outcomes in economic models.
- Chemistry - Chemists apply cubic equations to study reaction rates and equilibrium constants.
Understanding how to solve such equations is essential for professionals in these fields, as it allows them to make accurate predictions and informed decisions.
Exploring Variations of the Equation
While \( x^3 = 2 \) is the primary focus, there are variations and extensions of this equation that add depth to our understanding:
Example 1: \( x^3 = 8 \)
Consider the equation \( x^3 = 8 \). Solving for \( x \) involves taking the cube root of 8, resulting in \( x = 2 \). This example demonstrates how the cube root operation simplifies the equation and provides an exact solution.
Example 2: \( x^3 = 27 \)
Similarly, for \( x^3 = 27 \), the solution is \( x = 3 \). This illustrates the pattern that emerges when solving cubic equations with perfect cubes.
Example 3: Infinite Towers of \( x \)
Another fascinating variation involves the concept of an infinite tower of \( x \)'s. For example, if \( x^x^x = 2 \), the solution involves more advanced techniques, such as logarithms and iterative methods. This highlights the versatility and complexity of cubic equations.
Tools and Resources for Solving Cubic Equations
Modern technology offers numerous tools to assist in solving cubic equations:
- Online Calculators - Websites like Wolfram|Alpha provide powerful calculators that can solve cubic equations step by step.
- Mathematical Software - Programs like MATLAB and Mathematica offer advanced algorithms for solving complex equations.
- Mobile Apps - Many apps are designed specifically for solving algebraic equations, making them accessible to students and professionals alike.
These resources not only simplify the solving process but also enhance understanding by providing visual representations and step-by-step explanations.
Conclusion
The equation \( x^3 = 2 \) is a fascinating example of the complexity and beauty of algebra. By understanding the concept of cube roots and irrational numbers, we can unravel the mystery behind this equation and its variations. Its applications in engineering, physics, economics, and chemistry highlight the importance of mastering such mathematical principles.
In summary:
- The equation \( x^3 = 2 \) can be solved by isolating \( x \) and taking the cube root of 2.
- The solution, \( \sqrt[3]{2} \), is an irrational number approximately equal to 1.25992.
- This equation has practical applications in various fields, including engineering, physics, and economics.
- Modern tools and resources make solving cubic equations more accessible and efficient.
By exploring the depths of this equation, we gain a deeper appreciation for the power and elegance of mathematics.
Double & triple integral unit 5 paper 1 , B.Sc. 2 Mathematics | PPT
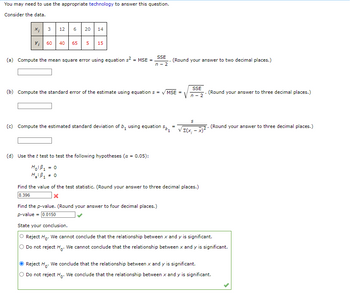
Answered: You may need to use the appropriate… | bartleby
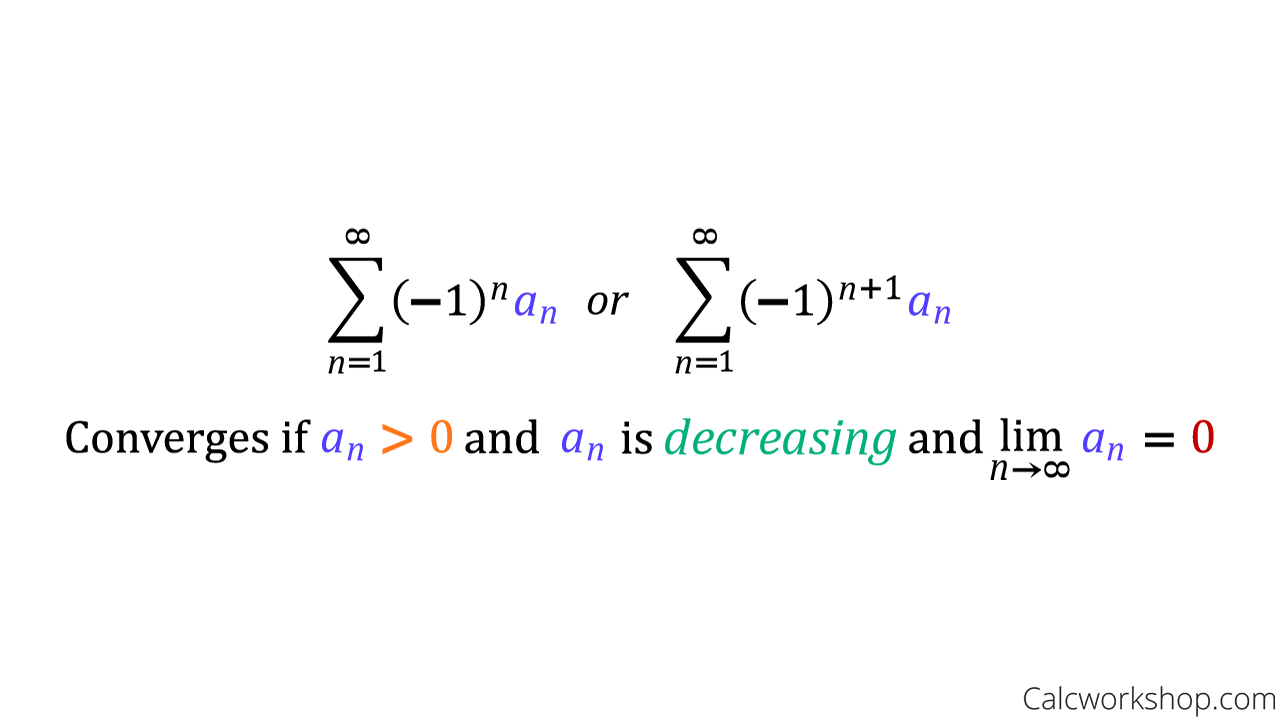
Alternating Series Estimation Theorem
