Mastering Perimeter Formulas: Your Guide To Measuring Shapes

Have you ever wondered how much fencing you need for your garden, or the exact distance you'd walk around a new park? These everyday questions, and countless others, hinge on a fundamental mathematical concept: perimeter. Understanding the perimeter formula isn't just for students in a classroom; it's a practical skill that empowers you to measure and plan in the real world. This comprehensive guide will demystify perimeter, providing clear explanations, essential formulas, and practical examples to help you master this crucial geometric concept.

From simple squares to complex irregular polygons, the ability to accurately calculate the perimeter is invaluable. Whether you're a student grappling with geometry homework, a DIY enthusiast planning a home improvement project, or simply curious about the world around you, this article will equip you with the knowledge to confidently determine the distance around any shape. We'll explore various perimeter formulas, discuss their real-world applications, and even highlight how modern tools can simplify these calculations, ensuring you gain a solid understanding of how to find the perimeter of different shapes using formulas and examples.

Understanding the Core Concept of Perimeter

At its heart, the concept of perimeter is remarkably simple yet profoundly important in mathematics and everyday life. In math, the perimeter of a shape is the total distance around the outer boundary of the shape. Imagine tracing the edge of any figure with your finger; the length of that path is its perimeter. Another way to describe the perimeter of a figure is the total measured length of the outline of the shape. It's literally "peri" (around) and "meter" (measure), so it's the measurement around something. The standard notation for perimeter is 'P'.

• Securely Connect Remote Iot Vpc Raspberry Pi Free
• Niks Indian
• Viralkandcom
• Viraljand
• Securely Connect Remoteiot Vpc Aws Raspberry Pi

The perimeter is the total length or distance around a two-dimensional shape. This distinguishes it clearly from "area," which is the space occupied by the boundaries of the figure. While area is about the surface inside, perimeter is exclusively about the boundary itself. For instance, if you're painting a wall, you'd calculate its area to know how much paint you need. But if you're putting decorative trim around that wall, you'd calculate its perimeter. Perimeter of any figure is measured in units of length, such as meters, feet, inches, or centimeters. This consistency in units is crucial for accurate calculations and practical applications. Understanding this fundamental distinction is the first step to mastering any perimeter formula.

To put it into a tangible perspective, consider the perimeter of a rectangular flower garden to be the length of the fence that surrounds the garden. You need to know this length to buy the correct amount of fencing material. On a larger scale, we can imagine a rectangular shaped park with a paved sidewalk surrounding it. The perimeter of the park would be the total distance that you would have to walk to travel the complete outer distance of the park (i.e., how far you would have to walk along the sidewalk to go around the park and end up back where you started). This real-world relevance underscores why learning how to calculate the perimeter of different shapes using formulas and examples is so beneficial.

The Universal Approach: Summing Up Sides

While different shapes have unique formulas for perimeter, there's a foundational principle that applies to almost all polygons: the perimeter is simply the sum of the lengths of all its sides. This is the most intuitive way to understand how to find the perimeter. If the figure is a polygon such as a triangle, square, rectangle, pentagon, or any other multi-sided shape, then the perimeter is the sum of the edge lengths of the polygon. This principle forms the basis for deriving specific perimeter formulas for regular shapes and for calculating the perimeter of irregular shapes.

• Aagmaalgives
• Xxxx Is Equal To 4x
• Necati Arabaci Mafia Boss
• Emily Carver Wikipedia
• Kid And His Mom Cctv Video Original Free

For example, if you have an irregular polygon with sides measuring 5 cm, 7 cm, 4 cm, and 6 cm, its perimeter would be 5 + 7 + 4 + 6 = 22 cm. It's as straightforward as adding up all the individual segments that make up the boundary. In essence, the perimeter of each shape is the sum of the lengths of each side. This concept is visually represented when you imagine walking along each side of a shape and adding up the distance covered on each segment until you return to your starting point. This universal approach is the bedrock upon which more specialized perimeter formulas are built, making it an essential concept to grasp before delving into specific geometric figures.

Essential Perimeter Formulas for Common 2D Shapes

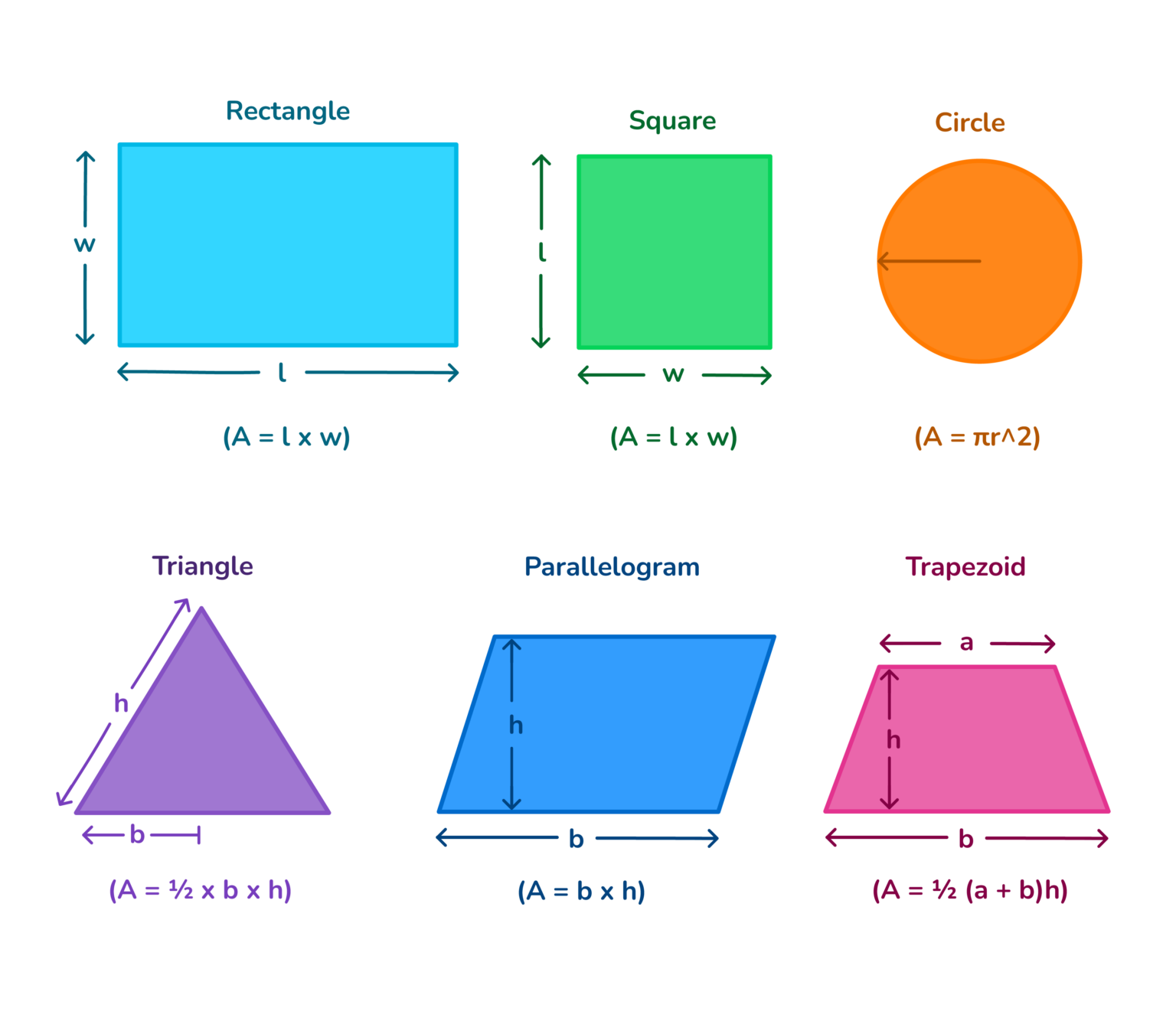
While the sum-of-sides method is universal for polygons, specific geometric shapes often have simplified perimeter formulas due to their inherent properties. These formulas make calculations quicker and more efficient. Learn the perimeter formulas for squares, rectangles, triangles, circles, ellipses, and more with examples and explanations. Mastering these core formulas is key to efficiently solving various mathematical and real-world problems. There are many types of shapes, the most common ones are square, triangle, rectangle, circle, etc. To know the area and perimeter of all these, we need different formulas. Let's dive into the most frequently encountered shapes.

Squares

A square is a four-sided polygon where all sides are equal in length, and all angles are right angles. Because all four sides are identical, calculating its perimeter is incredibly simple. If 's' represents the length of one side of a square, the perimeter formula for a square is:

P = 4s

This formula is derived from the basic principle of summing all sides: s + s + s + s = 4s. For example, a square with side length 3 units has a perimeter of 3 + 3 + 3 + 3 = 12 units. This can also be expressed as 4 × 3 = 12. This straightforward perimeter formula makes calculating the distance around square objects quick and easy.

Rectangles

A rectangle is also a four-sided polygon, but unlike a square, it has two pairs of equal-length sides: a length (l) and a width (w). The perimeter of a rectangle formula is the distance around the rectangle. Since opposite sides are equal, we can simplify the sum of all sides. We calculate the perimeter of a rectangle by getting the sum of all its sides.

P = 2(l + w) or P = 2l + 2w

This formula accounts for two lengths and two widths. For instance, if a rectangular garden is 10 meters long and 5 meters wide, its perimeter would be 2(10 + 5) = 2(15) = 30 meters. This is the length of the fence that surrounds the garden. This perimeter formula is widely used in construction, landscaping, and many other practical applications.

Triangles

A triangle is a three-sided polygon. Unlike squares and rectangles, triangles can have sides of varying lengths, making them more diverse. The most general perimeter formula for a triangle is simply the sum of the lengths of its three sides. If the sides are denoted as 'a', 'b', and 'c', the perimeter formula is:

P = a + b + c

For example, a triangle with sides measuring 3 cm, 4 cm, and 5 cm has a perimeter of 3 + 4 + 5 = 12 cm. While there are more complex rules for triangle calculation (like SSS, ASA, SAS, SSA for determining side lengths or angles), for finding the perimeter, the basic sum of sides remains the core principle. This fundamental perimeter formula applies to all types of triangles, whether equilateral (all sides equal), isosceles (two sides equal), or scalene (all sides different).

Circles (Circumference)

Circles are unique because they don't have straight sides. Therefore, their "perimeter" has a special name: the circumference. The perimeter of a circle is called the circumference. The circumference is the distance around the circle. The formula for the circumference involves pi (π), a mathematical constant approximately equal to 3.14159, and either the circle's radius (r) or diameter (d).

C = 2πr or C = πd

Remember that the diameter (d) is twice the radius (d = 2r). So, both formulas are essentially the same. Learn how to calculate the perimeter of a circle (circumference) using the formula 2πr or πd for accurate and easy measurements. For example, a circle with a radius of 7 cm would have a circumference of 2 × π × 7 ≈ 43.98 cm. This perimeter formula is critical in fields like engineering, physics, and architecture, where circular shapes are common.

Beyond the Basics: Polygons and Irregular Shapes

While squares, rectangles, triangles, and circles cover many common scenarios, the world of shapes is far richer. We also need to learn how to find the perimeter of regular and irregular shapes using formulas and examples. Polygons are multi-sided figures, and they can be regular (all sides and angles equal) or irregular (sides and angles vary). The good news is that the fundamental principle of summing all sides remains the most reliable perimeter formula for these more complex shapes.

For **regular polygons**, where all sides are equal, you can use a simplified perimeter formula similar to that of a square. If 'n' is the number of sides and 's' is the length of one side, the perimeter is:

P = n × s

For instance, a regular pentagon (5 sides) with each side measuring 3 units would have a perimeter of 3 + 3 + 3 + 3 + 3 = 15 units, which can be efficiently calculated as 5 × 3 = 15. Similarly, a regular octagon (8 sides) with a side length of 4 cm would have a perimeter of 8 × 4 = 32 cm. This generalized perimeter formula is incredibly useful for any regular polygon, from hexagons to decagons and beyond.

When it comes to **irregular shapes** or complex polygons where side lengths are not uniform, you simply revert to the most basic definition: the perimeter is the sum of the lengths of all the sides of the object. There's no single, neat perimeter formula for all irregular shapes; instead, you meticulously measure each segment of the boundary and add them together. This might involve breaking down a complex shape into simpler parts, or using a measuring tool to trace its entire outline. Even for shapes like parallelograms, trapezoids, or sectors of a circle, while they might have specific formulas for certain properties, their perimeter can always be found by summing the lengths of their boundary segments. This adaptability ensures you can find the perimeter of squares, rectangles, triangles, circles, polygons, and more, regardless of their regularity.

The Importance of Units and Avoiding Common Mistakes

Calculating perimeter isn't just about applying the correct perimeter formula; it's also about precision and attention to detail, especially concerning units of measurement. Perimeter of any figure is measured in units of length. This means if your side lengths are in meters, your perimeter will be in meters. If they are in inches, your perimeter will be in inches. A common mistake is to mix units within a single calculation (e.g., adding meters to centimeters without conversion), which will always lead to an incorrect result. Find out how to convert units and avoid common mistakes in math problems.

Here are some crucial tips to avoid common pitfalls:

• Unit Consistency: Always ensure all measurements are in the same unit before performing any calculations. If you have some sides in feet and others in inches, convert everything to either feet or inches first. For example, if one side is 2 feet and another is 18 inches, convert 2 feet to 24 inches (or 18 inches to 1.5 feet) before adding.
• Distinguishing Perimeter from Area: This is perhaps the most frequent mistake. Remember: perimeter is the distance around (measured in linear units), while area is the space inside (measured in square units). Confusing the two can lead to significant errors in practical applications, like ordering too much or too little material for a project.
• Using the Correct Formula: While the sum-of-sides works universally for polygons, using the specific perimeter formula for squares, rectangles, or circles is more efficient and less prone to errors for those shapes. Double-check that you're applying the right formula to the right shape.
• Accurate Measurement: In real-world scenarios, the accuracy of your perimeter calculation is only as good as the accuracy of your initial measurements. Use appropriate tools and techniques to measure sides precisely.
• Understanding Missing Information: Sometimes, not all side lengths are explicitly given. You might need to infer missing lengths from the properties of the shape (e.g., opposite sides of a rectangle are equal) or use other geometric principles.

By paying close attention to units and being mindful of these common mistakes, you can ensure your perimeter calculations are accurate and reliable, making your application of any perimeter formula much more effective.

Leveraging Online Tools for Perimeter Calculations

In today's digital age, you don't always need to manually crunch numbers to find the perimeter. Online tools and calculators have become incredibly valuable resources, especially for complex shapes or when you need quick, accurate results. An easy-to-use, free perimeter calculator can be a fantastic asset for students, professionals, and DIY enthusiasts alike. These tools can calculate the perimeter of shapes like square, rectangle, triangle, circle, parallelogram, trapezoid, ellipse, octagon, and even a sector of a circle.

The benefits of using these online calculators are numerous:

• Speed and Efficiency: Input your dimensions, and the calculator instantly provides the perimeter, saving you time and effort.
• Accuracy: These tools eliminate human error in calculations, ensuring precise results every time.
• Learning Aid: Many advanced calculators don't just give you the answer; they also provide formulas, explanations, and even graphs for each calculation. This can be a fantastic way to learn the formulas, explanations, and graphs for each calculation with examples and tips, reinforcing your understanding of the underlying mathematical principles.
• Versatility: They often support a wide range of geometric shapes, making them a versatile companion for various tasks. Use this online tool to calculate the perimeter of common geometrical shapes like square, rectangle, triangle, circle, and more.
• Unit Conversion: Some advanced calculators also offer built-in unit conversion features, helping you avoid one of the common mistakes discussed earlier.

While it's essential to understand the manual process and the underlying perimeter formula, these online resources serve as excellent verification tools and productivity enhancers. They allow you to find the perimeter of any geometric shape using this online tool quickly, making complex projects more manageable and ensuring accuracy in your measurements.

Practical Applications of Perimeter Formulas in Everyday Life

The concept of perimeter is far from an abstract mathematical exercise confined to textbooks. Finding the perimeter has many uses in everyday life, demonstrating its profound practical importance across various fields. Area and perimeter formulas have equal importance in real life for various calculations like finding the area of land or finding the perimeter of land for boundaries and many more. Here are just a few examples of how perimeter formulas are applied daily:

• Home Improvement and Gardening:
  • Fencing: As mentioned, determining how much fence you need for your yard or garden is a classic perimeter problem. You measure the boundary of your property or garden bed to calculate the total length of fencing required.
  • Baseboards and Crown Molding: When installing trim around a room, you need to calculate the perimeter of the room to know how many linear feet of material to purchase.
  • Landscaping Edging: Similarly, if you're putting decorative edging around a flower bed or walkway, the perimeter formula tells you how much material you'll need.
• Construction and Architecture:
  • Building Foundations: Architects and builders use perimeter calculations to determine the length of foundation walls, framing, and other structural components.
  • Room Layouts: Understanding the perimeter of rooms helps in planning furniture placement, carpet installation (though area is also critical here), and overall spatial design.
  • Material Estimation: From laying electrical conduits around a building's exterior to installing gutters, perimeter calculations are essential for estimating material quantities.
• Sports and Recreation:
  • Track and Field: Running tracks are designed with precise perimeters to ensure fair competition and consistent distances.
  • Sports Fields: The boundaries of sports fields (like soccer pitches, basketball courts) are defined by their perimeter, which must adhere to specific regulations.
• Fashion and Design:
  • Clothing Patterns: Tailors and fashion designers use perimeter concepts to measure necklines, waistbands, cuffs, and other edges of garments.
  • Crafts: Whether you're knitting a scarf, framing a picture, or creating a quilt, perimeter helps in determining the amount of yarn, frame material, or border fabric needed.
• Urban Planning and Mapping:
  • Property Boundaries: Surveyors use perimeter calculations to define property lines and land parcels.
  • City Planning: Understanding the perimeter of parks, districts, or even entire cities can be relevant for infrastructure planning, public services, and emergency response routes.

These examples highlight that the perimeter formula is not just an academic concept but a practical tool that underpins countless daily activities and professional endeavors. Learn how to calculate the perimeter of different 2D and 3D shapes using formulas and examples, and you unlock a valuable skill for problem-solving in the real world.

Mastering Perimeter: A Fundamental Skill

As we've explored, the journey from understanding what perimeter is to confidently applying various perimeter formulas is a crucial one. Area and perimeter formulas are the fundamental formulas in mensuration that help us calculate the area and perimeter for any geometric shape in mathematics. They are the building blocks for more advanced geometric concepts and have direct, tangible applications in our lives. From determining the length of a fence around a garden to understanding the dimensions of a running track, the ability to calculate perimeter is a foundational skill that transcends academic boundaries.

We've covered how to find the perimeter

• Demitra Kalogeras Age
• Xvideo The
• Maal49
• Anna Anon
• Remoteiot Vpc Ssh Windows 10

Details

Perimeter Formula Of A Triangle

Details

Area And Perimeter Formulas

Details

What is Perimeter in Math? - DoodleLearning