Understanding The Expression "x X X X Factor X(x+1)(x-4)+4x+1): A Comprehensive Guide
Introduction
Mathematics often presents us with complex expressions that can seem overwhelming at first glance. One such expression is "x x x x factor x(x+1)(x-4)+4x+1)." While this might look intimidating, breaking it down into simpler components makes it easier to understand. In this article, we will explore what this expression means, how to simplify or factor it, and the tools that can help you work with similar algebraic expressions. Whether you're a student, a teacher, or simply someone who enjoys solving math problems, this guide will provide you with the clarity you need.What Does Factoring Mean in Mathematics?
Factoring is a fundamental concept in algebra. It refers to the process of breaking down a mathematical expression into simpler components, called factors, whose product equals the original expression. For example, the expression \( x^2 - 4 \) can be factored as \( (x - 2)(x + 2) \). This process is essential for simplifying equations, solving for variables, and understanding the structure of polynomials.Why Factoring Matters
Factoring simplifies complex expressions, making them easier to work with. It also helps in finding solutions to equations. For instance: - **Finding Roots:** Factoring allows you to identify the roots or solutions of an equation. - **Simplifying Expressions:** Breaking down large expressions into smaller parts reduces complexity. - **Graphing:** Factored forms can help in visualizing the behavior of functions.Breaking Down the Expression
Let's now focus on the specific expression "x x x x factor x(x+1)(x-4)+4x+1)." At first glance, it appears complicated, but let's simplify it step by step.Step 1: Simplify the Expression
The given expression can be rewritten as: \[ x(x+1)(x-4) + 4x + 1 \] This is a polynomial involving multiple terms. To simplify it, we need to expand and combine like terms. Here's how: 1. Expand \( x(x+1)(x-4) \): - First, multiply \( (x+1)(x-4) \): \( x^2 - 4x + x - 4 = x^2 - 3x - 4 \). - Then, multiply by \( x \): \( x(x^2 - 3x - 4) = x^3 - 3x^2 - 4x \). 2. Add the remaining terms \( +4x + 1 \): - Combine \( -4x \) and \( +4x \): They cancel out. - The simplified expression becomes: \( x^3 - 3x^2 + 1 \).Step 2: Factor the Simplified Expression
Now that we have \( x^3 - 3x^2 + 1 \), the next step is to factor it. Factoring cubic polynomials can be challenging, but there are methods to simplify the process: - **Look for Common Factors:** In this case, there is no common factor. - **Use the Rational Root Theorem:** This theorem helps identify possible roots, which can then be used to factor the polynomial. While this polynomial doesn't have simple integer roots, advanced tools or calculators can help you find its factors.Tools and Resources for Factoring
Factoring complex expressions manually can be time-consuming and prone to errors. Fortunately, there are several tools and resources available to assist you:1. Factoring Calculators
Factoring calculators are powerful tools that simplify the process of breaking down complex expressions. They can: - Factor polynomials with multiple variables. - Find the greatest common divisor (GCD) or greatest common factor (GCF). - Simplify expressions step by step. Some popular factoring calculators include: - **Symbolab:** Offers detailed step-by-step solutions for a wide range of math problems, including factoring. - **Wolfram|Alpha:** A versatile tool that can factor polynomials, solve equations, and plot graphs. - **Mathway:** Provides solutions to algebraic problems, including factoring.2. Online Math Solvers
Online math solvers are excellent resources for solving equations, simplifying expressions, and factoring polynomials. These platforms often include: - **Step-by-Step Solutions:** Break down the process for better understanding. - **Graphing Capabilities:** Visualize the behavior of functions. - **Multiple Methods:** Use different approaches to solve problems.3. Graphing Calculators
Graphing calculators are particularly useful for visual learners. They allow you to: - Plot functions and observe their behavior. - Identify roots and intercepts. - Explore the relationship between factors and the graph of a polynomial.Steps to Factor an Expression
Factoring an expression doesn't have to be complicated. Follow these simple steps:Step 1: Write Down the Expression
Start by clearly writing the expression you want to factor. For example: \[ x(x+1)(x-4) + 4x + 1 \]Step 2: Simplify the Expression
Simplify the expression by expanding and combining like terms. In our example: \[ x^3 - 3x^2 + 1 \]Step 3: Identify Common Factors
Look for common factors in the terms of the expression. If no common factors exist, proceed to the next step.Step 4: Use Factoring Techniques
Apply factoring techniques such as: - **Grouping:** Group terms to find common factors. - **Difference of Squares:** Identify and factor expressions of the form \( a^2 - b^2 \). - **Cubic Factoring:** Use advanced methods to factor cubic polynomials.Step 5: Verify the Solution
Once you've factored the expression, verify your solution by multiplying the factors to ensure they equal the original expression.Conclusion
The expression "x x x x factor x(x+1)(x-4)+4x+1)" may initially seem daunting, but breaking it down into simpler components makes it manageable. Factoring is a crucial skill in algebra, helping to simplify expressions, solve equations, and visualize functions. By understanding the basics of factoring and utilizing available tools, you can tackle even the most complex mathematical problems with confidence. In summary: - Factoring simplifies expressions and reveals their underlying structure. - Tools like factoring calculators, online math solvers, and graphing calculators can assist in the process. - Following a systematic approach ensures accuracy and efficiency. Whether you're solving equations or exploring the behavior of functions, factoring remains an indispensable tool in mathematics. With practice and the right resources, you can master this skill and enhance your mathematical proficiency.
X X X X Factor X X 1 X 4 4 X 1 Meaning Means - Fill Online, Printable
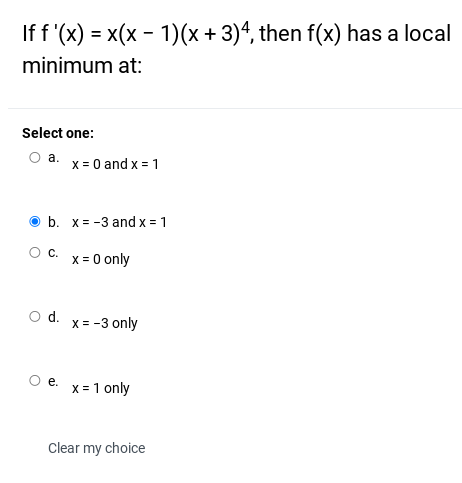
Solved If f'(x) = x(x - 1)(x + 3)4, then f(x) has a local | Chegg.com
^{4})
factor x^4-4x^3+6x^2-4x+1
